Pick and place with a KUKA youBot
The KUKA youBot is a mobile manipulator robot with four mecanum wheels and a 5R arm. In this project, the youBot is programmed to pick up a block, carry it to a new location, and put it down in simulation. This was done by modelling its kinematics, planning its reference trajectory, and using feedback + feedforward control to achieve it.
Video Demo
Kinematics Simulator
The NextState function, implemented in state_transition.py, takes the following inputs:
| Parameter | Description |
|---|---|
currentState |
12-vector representing the current robot configuration (3 for the chassis configuration, 5 for the arm configuration, and 4 for the wheel angles) |
controls |
9-vector of controls (4 for the wheel speeds, 5 for the arm joint speeds) |
dt |
Timestep |
speedlimit |
Maximum speed limit for the youBot |
and outputs a new 12-vector configuration after time dt has passed. The new arm joint and wheel angles are computed using a first-order Euler step, while the chassis configuration is updated using odometry estimates for a four-mecanum-wheel robot.
Trajectory Generation
The planner for the youBot end effector is implemented in trajectory_generator.py. It takes the following inputs:
| Parameter | Description |
|---|---|
Tse_init |
The initial end effector configuration |
Tsc_init |
The cube's initial configuration |
Tsc_final |
The cube's desired final configuration |
Tsc_final |
The end-effector configuration relative to the cube when grasping |
Tce_standoff |
The end effector's standoff configuration above the cube |
k |
The number of trajectory reference configurations per 0.01 seconds |
and outputs a list of flattened reference trajectories for inputting into the CoppeliaSim simulator. These trajectories are a mix of screw and Cartesian types generated with the help of the modern_robotics library.
Feedforward Control
The controller, implemented in controller.py, is based on a feedforward plus feedback control law.

The terms are:
| Parameter | Description |
|---|---|
X |
The current actual end effector configuration |
Xd |
The current end effector reference configuration |
Xerr |
The error twist |
Kp and Ki |
PI gain matrices |
V(d) |
The feedforward reference twist |
V(t) |
The commanded end effector twist |
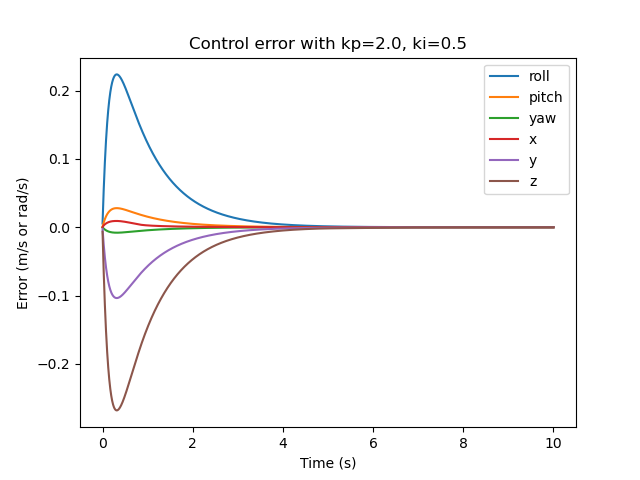
Results
The robot was successful at picking up the block and placing it at the desired position. There is no overshoot and the error twist decays rapidly.
Check out the project → GitHub
